Bahas Soal Matematika   »     ›  

Tentukan hasil dari \(\int \csc^3 x \ dx = \cdots ? \)

Pembahasan:

Untuk menyelesaikan integral ini kita uraikan fungsi \( \csc^3 x \) menjadi \( \csc x \cdot \csc^2 x \). Lalu berdasarkan rumus identitas trigonometri, ganti fungsi \( \csc^2 x \) menjadi \( (1+\cot^2 x) \). Kita peroleh hasil berikut:

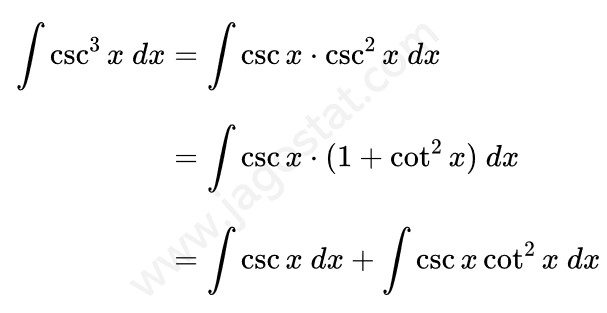
Dari hasil di atas, sekarang kita akan mencari \( \int \csc x \ dx \) dan \( \int \csc x \cot^2 x \ dx \). Kita sudah pernah mencari integral \( \int \csc x \ dx \) di mana hasilnya yaitu \( \int \csc x \ dx = \ln|\csc x - \cot x| + C \) dan untuk integral \( \int \csc x \cot^2 x \ dx \) dapat kita selesaikan menggunakan teknik integral parsial dengan memisalkan \( u = \cot x \) dan \( dv = \csc x \cot x \ dx \) sehingga kita peroleh:

Dengan demikian, integral dari \( \csc^3 x \), yakni:

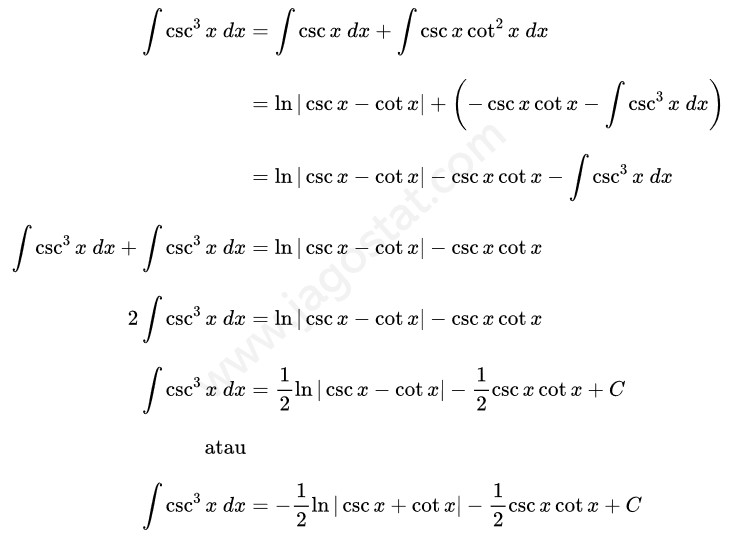
Rumus Integral Trigonometri Berpangkat

Berikut ini adalah beberapa rumus terkait integral trigonometri berpangkat:

Untuk integral trigonometri pangkat yang lebih tinggi kita dapat gunakan rumus reduksi berikut ini. Untuk pembuktiannya klik ini: Rumus Reduksi Integral Trigonometri